CBSE Sample Papers for Class 12 Physics Set 5 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 12 Physics with Solutions Set 5 are designed as per the revised syllabus.

CBSE Sample Papers for Class 12 Physics Set 5 with Solutions

Time : 3 hrs
Max. Marks : 70

Instructions
1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary.
(i) c = 3 × 10⁸ m/s
(ii) m_e = 9.1 × 10^-31 kg
(iii) e = 1.6 × 10^-19 C
(iv) µ₀ = 4π × 10^-7 TmA× 10^-1
(v) h = 6.63 × 10^-34 Js
(vi) ε₀ = 8.854 × 10^-112 C²N^-1m^-2
(vii) Avogadro’s number = 6.023 × 10²³ per gram mole

Section A

Question 1.
A magnet is brought towards a coil (i) speedily (ii) slowly, then the induced emf /induced charge will be respectively [1]
(a) more in first case/more in first case
(b) more in first case/equal in both case
(c) less in first case/more in second case
(d) less in first case/equal in both case
Answer:
(b) Magnitude of induced emf is directly proportional to the rate of change of magnetic flux. Induced charge doesn’t depend upon time.

Question 2.
The two similar bar magnet P and Q, each of magnetic moment M, are taken. If P is cut along its axial line and Q is cut along its equatorial line, all the four pieces obtained have [1]
(a) equal pole strength
(b) magnetic moment
(c) magnetic moment
(d) magnetic moment M
Answer:
(c) magnetic moment

If pole strength, magnetic moment and length of each part are m’, M’ and L’ respectively, then
(m’)_P =\(\frac{m}{2}\) (m’)_Q = m
(L’)_P = L (L’)_Q = \(\frac{L}{2}\)
⇒ (M’)_P = \(\frac{M}{2}\)
⇒ (M’)_Q = \(\frac{M}{2}\)

Question 3.
A wire of length L (= 20 cm) is bent into a semi-circular arc. If the two equal halves of the arc were each to be uniformly charged with charges ± Q (Here, |Q| = 10³ ε₀), then the net electric field at the centre O of the semi-circular arc would be [1]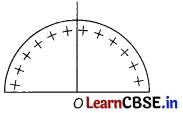

(a) 25 × 10³ N/C
(b) 50 × 10³ N/C
(c) 25 × 10³ N/C
(d) 50 × 10³ N/C
Answer:
(a) 25 × 10³ N/C

The electric field at the centre of a semicircular charged wire is given by

Question 4.
In photoelectric effect experiment, collector plate is made negative with respect to emitter plate as shown in figure till it reaches a certain potential V₀, when photocurrent is zero.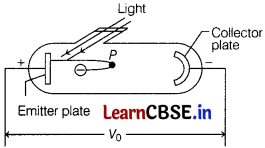

If K indicates kinetic energy of an emitted photoelectron, then at point P
(a) K > eV₀
(b) K < eV₀
(c) K = eV₀
(d) 0 ≤ K ≤ eV₀
Answer:
(c) K = eV₀

In the given condition, photocurrent is zero when the stopping potential is sufficient to repel even the most energetic photoelectrons, with the maximum kinetic energy K, so that K = eV₀.
Thus, at point P (as shown in the given figure), it can be seen clearly that the electron must have been repelled, so maximum kinetic energy, K = eV₀.

Question 5.
Which of the following statement is incorrect? [1]
(a) Electromagnetic waves cannot be deflected by any field.
(b) The velocity of light in a medium is v = \(\frac{1}{\sqrt{\mu \varepsilon}}\), thus it depends on both the electric and magnetic properties of the medium.
(c) The constant velocity of electromagnetic waves in vacuum is used to define a standard of time.
(d) The direction of propagation vector k describes the direction of propagation of the wave.
Answer:
(c) The constant velocity of electromagnetic waves in vacuum is used to define a standard of time.

The statement in option (c) is incorrect and it can be corrected as,
The constancy of the velocity of electromagnetic waves in vacuum is used to define a standard of length. The meter is defined as the distance travelled by light in vacuum in a time (1/c)second.

Question 6.
If the orbital radius of the electron in a hydrogen atom is 4.7 × 10¹¹H m, compute the kinetic energy of the electron in hydrogen atom. [1]
(a) 15.3 eV
(b) -1.53 eV
(c) 13.6 eV
(d) -13.6 eV
Answer:
(a) 15.3 eV

Kinetic energy,
K = \(\frac{e^2}{8 \pi \varepsilon_0 r}\) = \(\frac{9 \times 10^9 \times\left(1.6 \times 10^{-19}\right)^2}{2 \times 4.7 \times 10^{-11}}\)
= 2.45 × 10¹⁸ J = 15.3 eV (∵ 1 eV = 1.6 × 10^-19 J)

Question 7.
Two circular coils can be arranged in any of the three situations as shown in the figure below. Their mutual inductance will be [1]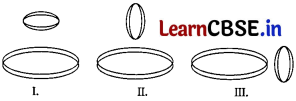

(a) maximum in situation I
(b) maximum in situation II
(c) maximum in situation III
(d) the same in all situations
Answer:
(a) maximum in situation I

Mutual inductance between two coils depends on their flux linkage, i.e. the fraction of flux linked with one coil which is produced when some current passes through the other coil. In situation (I), two coils have their planes parallel to each other. In this situation, maximum flux passes. Hence, maximum mutual inductance will be in situation (I).

Question 8.
Consider the situation shown in figure below. The capacitor P has charge q on it, whereas Q is uncharged.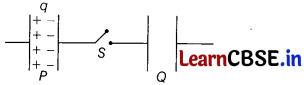

The charge appearing on the capacitor Q a long time after the switch S is closed, is [1]
(a) zero
(b) q
(c) q/2
(d) 2q
Answer:
(a)

When switch S is closed, there will be no transfer of charge from capacitor P to capacitor Q because the charge -q of P is held by its charge +q.

Question 9.
V-I characteristics of a silicon diode is as shown. [1]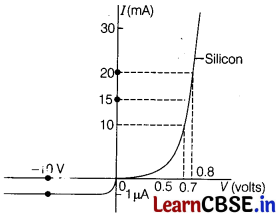

The ratio of resistance of diode at I_D = 15 mA and V_D = -10 V, is
(a) 10^-3
(b) 10^-4
(c) 10^-5
(d) 10^-6
Answer:
(d) 10^-6

From the graph, given in question at
I = 20 mA, V = 0.8 V and at I = 10 mA, V = 0.7 V

Question 10.
In Rutherford’s a-particle scattering experiment, what will be the correct angle for a scattering for an impact parameter b = 0 ? [1]
(a) 90°
(b) 27°
(c) 0°
(d) 180°
Answer:
(d) 180°

When b = 0, scattering angle, θ = 180°.

Question 11.
Biot-Savart law indicates that the moving electron (velocity v) produce a magnetic field a such that [1]
(a) B ⊥ v
(b) B || v
(c) it obeys inverse cube law
(d) it is along with the line joining, the electron and point of observation.
Answer:
(a) B ⊥ v

Magnetic field is given by, B = \(\frac{\mu_0}{4 \pi}\) |q| \(\frac{(\mathbf{v} \times \mathbf{r})}{\left|r^3\right|} \hat{\mathbf{n}}\)

where \(\hat{\mathbf{n}}\) is the direction of B which is in the direction of cross product of v and r.

Question 12.
Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B = B₀k. [1]
(a) They have equal Z-component of momenta.
(b) They must have equal charges.
(c) They necessarily represent a particle anti-matter or anti-particle pair.
(d) The charge to mass ratio satisfy
\(\left(\frac{e}{m}\right)_1\) + \(\left(\frac{e}{m}\right)_2\) = 0
Answer:
(a) They have equal Z-component of momenta.

The charge to mass ratio satisfy by
\(\left(\frac{e}{m}\right)_1\) + \(\left(\frac{e}{m}\right)_2\) = 0, here, charge/mass ratio of these two particles are same and charge on them are of opposite nature for traverse identical helical paths.

For questions 13 to 16 two statements are given-one labelled
Assertion (A) and other labelled Reason (R).
Select the correct answer to these questions from the options as given below.
(a) If both A and R are true and R is the correct explanation of A.
(b) If both A and R are true but R is not the correct explanation of A.
(c) If A is true but R is false.
(d) If both A and R are false.

Question 13.
Assertion (A) Induced emf will always occur, whenever there is change in magnetic flux.
Reason (R) Current always induces, whenever there is change in magnetic field. [1]
Answer:
(c) If A is true but R is false.

Emf will always be induced, whenever there is change in magnetic flux. The current will induced only in a closed loop.

Question 14.
Assertion (A) A capacitor is connected to a direct current source. Its reactance is infinite.
Reason (R) Reactance of a capacitor is given by X_C = \(\frac{1}{\omega C}\). [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.

For DC source, f = 0
X_C = \(\frac{1}{\omega C}\) = \(\frac{1}{2 \pi f C}\)
= \(\frac{1}{0}\) = ∞

Question 15.
Assertion (A) The image of a point object situated at the centre of hemisphere lens is also at the centre.
Reason (R) For hemisphere, Snell’s law is not valid. [1|
Answer:
(c) If A is true but R is false.

The ray from centre of hemisphere cut at the centre after refraction. Snell’s law is valid in each case of refraction.

16. Assertion (A) Though light of a single frequency (monochromatic) is incident on a metal, the energies of emitted photoelectrons are different.
Reason (R) The energy of electron emitted from inside the metal surface, is lost in collision with the other atom in the metal. [11
Answer:
(a) If both A and R are true and R is the correct explanation of A.

When a light of single frequency falls on the electrons of inner layer of metal, then this electron comes out of the metal surface after a large number of collision with atom of its upper layer.

Section B

Question 17.
A cell of emf E and internal resistance r is connected across a variable resistor R as shown below.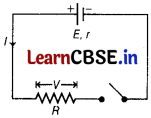

(i) Plot a graph showing the variation of terminal potential V with resistance R. [1]
(ii) Predict from the graph, the condition under which V becomes equal to E. [1]
Answer:
(i) From the given diagram,
V = IR = \(\frac{E}{R+r}\) ⋅ R = \(\frac{\frac{E}{\frac{R+r}{R}}\)
V = \(\frac{E}{1+\frac{r}{R}}\)
When R = 0, V = 0
When R = r, V = \(\frac{E}{2}\)
When R = ∞, V = E
The plot showing variation of V versus ft is given below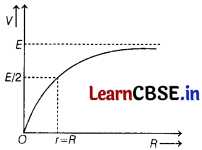

(ii) From the above graph, it is clear that V becomes equal to E when R → ∞.

Question 18.
The electrical conductivity of a semiconductor increases when electromagnetic radiation of a wavelength shorter than 2480 nm is incident on it. Find band gap in (eV) for the semiconductor. [2]
Answer:
Band gap = Energy of photon at λ = 2480 nm

Question 19.
When a certain photosensitive surface is illuminated with monochromatic light of frequency f, the stopping potential for the photocurrent is (\(\frac{V_0}{2}\)) When the surface is illuminated by monochromatic light of frequency f/2, the stopping potential is -V₀. Find the threshold frequency for photoelectric emission. [2]
Answer:
According to first condition, hf = ϕ + (\(\frac{V_0}{2}\))e ……….(i)
According to second condition,
\(\frac{hf}{2}\) = ϕ + V₀e ………(ii)
From Eqs. (i) and (ii), we get
(\(\frac{1}{2}\)) = \(\frac{(hf-\phi)}{\left(\frac{h f}{2}-\phi\right)}\)
hf₀ = (\(\frac{3}{2}\)) hf
⇒ f₀ = (\(\frac{3}{2}\)) f

Question 20.
A convex lens is put 10 cm from a light source and it makes a sharp image on a screen, kept 10 cm from the lens. Now a glass block (refractive index 1.5) of 1.5 cm thickness is placed in contact with light source. To get the sharp image again, the screen is shifted by a distance d. Calculate the distance between screen and slit. [2]
Answer:
Case I
u = -10 cm, v = 10 cm, f =?
Using lens formula, \(\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\)
\(\frac{1}{f}\) = \(\frac{1}{10}\) + \(\frac{1}{10}\) = f = 5 cm

Case II
Due to introduction of slab shift in source
= t[1 – \(\frac{1}{\mu}\)] = 1.5 [1 – \(\frac{2}{3}\)] = 0.5
Now, u = – 9.5 cm, v = 10.55 cm,
d = 10.55 – 10
d = 0.55 cm away from the lens.

Question 21.
Three light rays, red (R), green (G) and blue (B) are incident on a right angled prism ABC at face AB. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively.
(i) Find the critical condition of refractive index of prism. [1]
(ii) Out of the three, red colour ray will emerge from AC. Justify this observation. [1]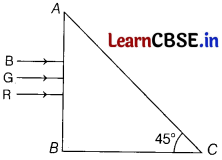

Or
Show that a light ray will pass through an equilateral glass prism (μ = 1.5), if the angle of incidence is greater than 30°. [2]
Answer:
(i) By geometry, angle of incidence (i) at face AC for all three rays is 45°. As we know, light suffers total internal reflection for which this angle of incidence is greater than critical angle. i > i_c
⇒ sin i > sin i_c

or sin 45° > sin i_c
or \(\frac{1}{\sin 45^{\circ}}\) < \(\frac{1}{\sin i_C}\) ⇒ μ > √2 or 1.414 [∵ sin i_c = 1/μ]

(ii) Since, total internal reflection takes place on face AC for rays with μ > √2 = 1.414. Hdnce, green and blue colours suffers total internal reflection whereas red undergoes refraction. Thus, out of three only red colour ray will emerge from AC.

Or

From Snell’s law, μ = \(\frac{\sin i}{\sin r}\)
If the light is incident at 30°, then
sin r = \(\frac{\sin i}{\mu}\) = \(\frac{\sin 30^{\circ}}{1.5}\)
= \(\frac{0.5}{1.5}\) = 0.33
⇒ r = sin^-1(0.33) = 19°
Angle of incidence at second face,
i’ = A – r
= 60°- 19° = 41°
which is just less than the critical angle 42° for glass-air interface. If i < 30°, then r’ > i_c and the ray will suffer total internal reflection at the second face and will not emerge through the prism.

Section C

Question 22.
Two point charges 3.4μ C and -2.0μ C are placed 5.0 cm apart on X-axis. At what points on X-axis, electric potential is zero? [3]
Answer:
There are two possible locations where potential can be zero. Now, as potential due to positive charge is positive and due to negative charge is negative and we can use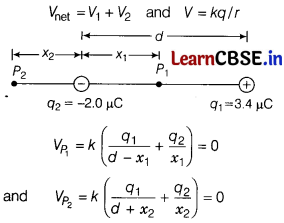

Solving these equations, we get
x¹ = 1.852 cm and x² = 7.143 cm
So, there are 2 locations where potential is zero.

Question 23.
Consider a uniform electric field E =3 × 10³ \(\hat{\mathbf{i}}\) NC^-1.
(i) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the YZ-plane? [2]
(ii) What is the flux through the same square, if the normal to its plane makes a 60° angle with the X-axis? [1]
Answer:
(i) Area of square, A = a² = 10² = 100 cm²
= 100 × 10^-4 m²
Now, A =(10² \(\hat{\mathbf{i}}\))m²
Electric flux through the square,
ϕ = EA cosθ = (3 × 10³ \(\hat{\mathbf{i}}\)) ⋅ (10^-2 \(\hat{\mathbf{i}}\)) = 3 × 10¹
ϕ = 30 N-m²C^-1

(ii) When normal to plane i.e. A makes angle 60° with E
ϕ’ = EA cos 60°
= 3 × 10³ × 10^-2 × \(\frac{1}{2}\) = 15 N-m²C^-1

Question 24.
(i) In accordance with the Bohr’s model, find the quantum number that characterises the earth’s revolution around the sun in an orbit of radius 15 × 10¹¹ m with orbital speed 3 × 10⁴ m/s.
(Mass of the earth = 6.0 × 10²⁴ kg). [1]
(ii) A difference of 2.3 eV separates two energy level in antom. What is the frequency of radiation emitted when the atom makes a transition from the upper level to the lower level? [2]
Answer:
(i) Angular momentum of the earth around the sun,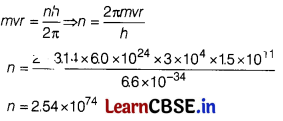

(ii) Given,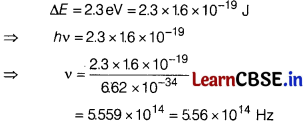

Question 25.
In a discharge tube, the number of hydrogen ions drifting across a cross-section per second is 10 × 10¹⁸, while the number of electron drifting in opposite direction across another cross-section is 2.7 × 10¹⁸ per second. If the supply voltage is 230 V, what is the effective resistance of the tube? [3]
Answer:
Total current is sum of current due to electron and current due to protons.

Question 26.
(i) State Biot-Savart law. [2]
(ii) A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire? [1]
Answer:
(i) Biot-Savart law states that the magnetic field due to a tiny current element at any point is directly proportional to the length of current element, the current, the sine of angle between the direction of current element and the point and inversely proportional to the square of distance between them.
dB = \(\frac{\mu_0}{4 \pi}\) × \(\frac{I d / \sin \theta}{r^2}\)

(ii) Magnetic field due to a long straight wire,
B = \(\frac{\mu_0}{4 \pi}\) × \(\frac{2l}{r}\) = B = 10^-7 × \(\frac{2 \times 35}{20 \times 10^{-2}}\)
⇒ B = 3.5 × 10^-5 T

Question 27.
A plane electromagnetic wave of frequency 25 MHz travels in free space along the x-direction. At a particular point in space and time, E = 6.3 \(\hat{j}\) V/m. What is B at this point?
Answer:
The magnitude of B is
B = \(\frac{E}{c}\) = \(\frac{6.3 \mathrm{~V} / \mathrm{m}}{3 \times 10^8 \mathrm{~m} / \mathrm{s}}\) = 2.1 × 10^-8 T
To find the direction, we note that E is along Y-direction and the wave propagates along X-axis. Therefore, B should be in a perpendicular to both X and Y-axes.
Thus, B = 22.1 × 10^-8 \(\hat{j}\) T

Question 28.
Use Lenz’s law to determine the direction of induced current in the situations described by figure.
(i) A wire of irregular shape turning into a circular shape.
(ii) A circular loop being deformed into a narrow straight wire. [3]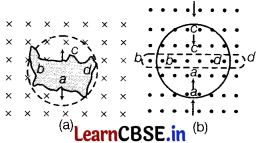

Or
A metallic rod of length l is moved perpendicular to its length with velocity v in a magnetic field B acting perpendicular to the plane in which rod moves. Derive the expression for the induced emf. [3]
Answer:
(i) Here, the direction of magnetic field is perpendicularly inwards to the plane of paper.
If a wire of irregular shape turns into a circular shape, then its area increases (therefore the circular loop has greater area than the loop of irregular shape), so that the magnetic flux linked also increases. Now, the induced current is produced in a direction such that it decreases the magnetic field, i.e. the current will flow in such a direction, so that the wire forming the loop is pulled inward in all directions (to decrease the area), i.e. current is in anti-clockwise direction, i.e. along adcba.

(ii) When a circular loop deforms into a narrow straight wire, the magnetic flux linked with it also decreases. The current induced due to change in flux will flow in such a direction that it will oppose the decrease in magnetic flux, so it will flow anti-clockwise, i.e. along adcba due to which the magnetic field produced will be out of the plane of paper.

Or

Consider a uniform magnetic field B confined to the region ABCD and a coil PQRS is placed inside the magnetic field. At any time t, the part P’Q – S’R = y of the coil is inside the magnetic field. Let l be the length of the arm of the coil.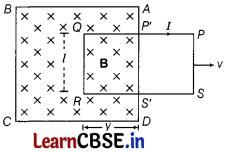

Area of the coil inside the magnetic field at time t,
∆S =QR × RS’ = ly
Magnetic flux linked with the coil at any time t,
ϕ = B∆S = Bly
The rate of change of magnetic flux linked with the coil is given by
\(\frac{d \phi}{d t}\) = \(\frac{d}{dt}\) (Bly)
= Bl \(\frac{d y}{d t}\) = Blv
where, v is the velocity with which the coil is pulled out of the magnetic field.
If e is the induced emf, then according to Faraday’s law,
e = \(-\frac{d \phi}{d t}\) or e = -Blv

Section D
[Case Study Based Questions]

Question 29.
Read, the following paragraph and answer the questions that follow
Consider the arrangement shown in figure. Let A and B be two thin lenses of focal lengths f₁ and f₂ placed coaxially in contact with each other. Note that the lenses themselves may be convex or concave and this is captured in signs of f₁ and f₂.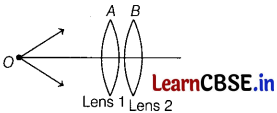

\(\frac{1}{f_e}\) = \(\frac{1}{f_1}\) + \(\frac{1}{f_2}\)
where, f₁ and f₂ are focal lengths of two lenses and \(\frac{1}{f}\) = \(\frac{1}{v}\) + \(\frac{1}{u}\).

(i) The combination of lenses as shown in figure. Lenses A and B having focal lengths 10 cm and -20cm respectively, then lateral magnification is [1]
(a) 2
(b) 4
(c) 8
(d) 5
Answer:
(a) 2

We know that,

(ii) If a set of n thin lenses are placed next to each other such that the distance between the lenses is zero, then the net focal length of system is [1]
(a) \(\frac{1}{f_net}\) = \(\sum_{i=1}^n \frac{1}{f_i}\)
(b) f_net = \(\sum_i \frac{1}{f_i}\)
(c) f_net = 0
(d) None of these
Answer:
(a) \(\frac{1}{f_net}\) = \(\sum_{i=1}^n \frac{1}{f_i}\)

(iii) Total magnification of combination given in part (ii) will be given by [1]
(a) m_eff = \(\frac{1}{m_1}+\frac{1}{m_2}+\frac{1}{m_3}+\ldots+\frac{1}{m_n}\)
(b) m_eff = \(m_1 \times m_2 \times m_3 \times \ldots \times m_n\)
(c) m_eff = \(\frac{1}{m_1} \times \frac{1}{m_2} \times \frac{1}{m_3} \ldots \frac{1}{m_n}\)
(d) None of the above
Answer:
(b) m_eff = \(m_1 \times m_2 \times m_3 \times \ldots \times m_n\)

Or

If two thin lenses of opposite nature with different focal lengths are put in contact, the resultant focal length will be [l]
(a) same nature as that of lens of shorter focal length
(b) different nature as that of lens of shorter focal length
(c) same nature as that of lens of larger focal length
(d) different nature as that of lens of larger focal length
Answer:
(a) same nature as that of lens of shorter focal length

When two thin lenses of opposite nature with different focal length are put in contact, the resultant focal length is same nature as that of lens of shorter focal length.

(iv) If two thin lenses of equal focal length but of opposite nature are put in contact, the resultant focal length of the combination will be [1]
(a) \(\frac{1}{f_res}\) = \(\frac{1}{f}\) + \(\frac{1}{(-f)}\)
(b) \(\frac{1}{f_res}\) = \(\frac{1}{f}\) + \(\frac{1}{f}\)
(c) \(\frac{1}{f_res}\) = ∞
(d) None of these
Answer:
(a) \(\frac{1}{f_res}\) = \(\frac{1}{f}\) + \(\frac{1}{(-f)}\)

\(\frac{1}{f_res}\) = \(\frac{1}{f}\) + \(\frac{1}{(-f)}\) = 0
i.e. f_res = ∞ and P = 0
i.e. the system will behave as plane glass plate.

Question 30.
Read the following paragraph and answer the questions that follows
p-n Junction
In an n-type semiconductor, the concentration of electrons is more than that of holes. Similarly in a p-type semiconductor, the concentration of holes is more than that of electrons. During the formation of p-n junction and due to the concentration gradient across p and n-type, holes diffuse from p-side to n-side and electron diffuse from n-side to p-side.

(i) The maximum energy point of the electrons at absolute zero is called [1]
(a) fermi energy
(b) emission energy
(c) work function
(d) potential energy
Answer:
(a) fermi energy

The maximum energy point of the electrons at absolute zero is called fermi energy.

(ii) A p-n junction diode cannot be used [1]
(a) for converting light energy’ to electrical energy
(b) for concerting light energy to electrical energy
(c) for getting light radiation
(d) for increasing the amplitude of an AC signal
Answer:
(d) for increasing the amplitude of an AC signal

Diode cannot be used for the purpose of amplification.

(iii) Barrier potential of a p-n junction diode does not depend on [1]
(a) diode design
(b) temperature
(c) forward bias
(d) doping density
Answer:
(a) diode design

The barrier potential depends upon temperature, forwards bias and doping density.

(iv) Reverse bias applied to a junction diode [1]
(a) lowers the potential barrier
(b) raises the potential barrier
(c) increases the majority carrier current
(d) increases the minority carrier current
Answer:
(b) raises the potential barrier

The reverse bias oppose the movement of majority charge carriers. Thus, with the increase of reverse biasing potential barrier increases.
Or

The p-n junction diode is used as [1]
(a) an amplifier
(b) a rectifier
(c) an oscillator
(d) a modulator
Answer:
(b) a rectifier

It is used to convert AC into DC (rectifier).

Section E

Question 31.
(i) Find an expression for the torque acting on an electric dipole placed in uniform electric field. [3]
(ii) A system of two charges
q_A = 2.5 × 10^-7C and q_B = -2.5 × 10^-7C located at points A (0,0,-15)cm and B (0,0,+15) cm, respectively. Find
(a) the electric dipole moment of the system and
(b) the magnitude of the torque acting on it, when it is placed in a uniform electric field 5 × 10⁴ NC× 10^-1, making an angle of 30°, with the Z-axis. [2]
Answer:
(i) Consider an electric dipole AB which consists of two point charges +q and -q, separated by a distance 2a. It is placed in a uniform electric field E, making an angle θ.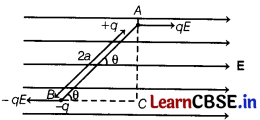

Force acting on charge +q,
F₁ = qE [along the direction of E ]
Force acting on charge -q,
F₂ = qE [opposite to the direction of E]
Forces F₁, and F₂ are equal in magnitude and opposite in direction having different lines of action of force. Therefore, it forms a couple of force. Torque acting on dipole = Force × Perpendicular distance between the forces
τ = qE × AC
From ∆ACB, sinθ = AC/AB
or AC = AB sinθ or AC = 2a sinθ
∴ τ = qE × 2a sinθ
But q × 2a = p [electric dipole moment]
∴ τ = pE sinθ or τ = p × E

(ii) (a) Here, charges, |q_A| = |q_B| = 2.5 × 10^-7 C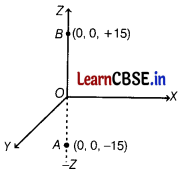

Length of dipole = 2a = 30 cm = 0.30 m
∴ Electric dipole moment (p) = q (2a)
= 2.5 × 10^-7 × 0.30 =7.5 × 10^-8 C-m
This dipole moment p is along the negative Z-axis.

(b) Given, uniform electric field, E = 5 × 10⁴ NC× 10^-1
Angle, θ = 30°
∴ Torque acting on electric dipole,
τ = pE sinθ = 7.5 × 1O-8 × 5 × 104 × sin30°
= 37.5 × 10^-4 × 1/2
= 18.75 × 10^-4
= 1.88 × 10^-3 N-m

Or

A capacitor of capacitance C is charged fully by connecting it to a battery of emf E. It is then disconnected from the battery. If the separation between the plates of the capacitor is now doubled, what will happen to [5]
(i) capacitance of the capacitor?
(ii) charge stored by the capacitor?
(iii) potential difference across it?
(iv) field strength between the plates?
(v) energy stored by the capacitor?
Sol.
(i) Capacitance of the capacitor,
C = \(\frac{1}{2}\) ⇒ C ∝ \(\frac{1}{d}\)
When separation between the plates is doubled, the capacitance is reduced to half of its initial value.
(ii) Charge stored by the capacitor would remain unchanged.
(iii) Potential difference between the plates, V = q/C
As, capacitance of the capacitor (C = K Aε₀/d) reduces to half, hence potential difference between the plates becomes twice of the initial value, i.e. 2 V.
(iv) Field strength between the plates, E = V/d
E = \(\frac{2V}{2d}\) = \(\frac{V}{d}\)
Thus, it remains same as E.
(v) Energy stored by the capacitor, U = \(\frac{1}{2}\)\(\frac{q^2}{C}\)
As, capacitance reduces to half and charge remains same, hence energy stored would be doubled.

Question 32.
(i) Using the data given below, state which two of the given lenses will you prefer to construct a best possible [3]
(a) telescope and
(b) compound microscope.
Also, indicate which of the selected lenses is to be used as an objective and as an eyepiece in each case.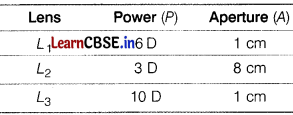

(ii) You are given two converging lenses of focal length 1.25 cm and 5 cm to design a compound microscope. If it is desired to have a magnification of 30, then find out the separation between the objective and eyepiece. [2]
Answer:

Or

(i) With the help of a ray diagram, show the formation of image of a point object by refraction of light at a spherical surface separating two media of refractive indices n₁ and n₂(n₂ > n₁), respectively. [3]
(a) Using a diagram, derive the relation
\(\frac{n_2}{v}\) – \(\frac{n_1}{u}\) = \(\frac{n_2-n_1}{R}\)
(b) Write the sign conventions used.
(ii) An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change, if the lens is reversed? [2]
Answer:
(i) Power of lens, P = \(\frac{1}{\text { Focal length, } f \text { (in } \mathrm{m})}\)
⇒ f = 1/ P or f(in cm) = 100/P
∴ Focal lengths of three lenses are as follows
f₁ =16.67 cm, f₂ = 33.33 cm and f₃ = 10 cm

(a) For telescope: Objective should be of large aperture and large focal length, so lens L₂ is fit for objective. Eyepiece should be of small aperture and small focal length, so lens L₃ is fit for making eyepiece.
(b) For compound microscope: Objective must be of small aperture and small focal length and therefore, lens L₃ can be used for objective.
Eyepiece must be of small aperture and larger focal length as compare to objective. Thus, lens L₁ is fit for making eyepiece.

(ii) Given, f₀ = 125 cm, f_e = -5cm Magnification, m = 30, D = 25 cm
If the object is very close to the principal focus of the objective and the image formed by the objective is very close to eyepiece, then magnifying power of a microscope is given by
m = –\(\frac{L}{f_0}\) . \(\frac{D}{f_e}\)
⇒ 30 = \(\frac{L}{125}\) . \(\frac{25}{5}\)
⇒ L = \(\frac{125×30×5}{25×100}\)
⇒ L = \(\frac{25×30}{100}\) ⇒ L = \(\frac{30}{4}\)
⇒ L = 7.5 cm
This is a required separation between the objective and the eyepiece.

Or

(i) (a) Let a point object O be placed at a distance u from the pole in a medium of refractive index n₁ outside the spherical refracting surface of radius of curvature R. Its real image I is formed at a distance v in denser medium of refractive index n₂. Here, angle of incidence is i and angle of refraction is r.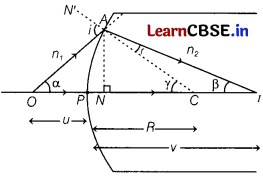

Draw a normal AN on principal axis.
Let ∠AOC = α, ∠AIC = ß,
∠ACO = γ
For ∆AOC,i is the exterior angle
i = α + γ ……..(i)
For ∆AIC, γ is the exterior angle
.-. γ = r + ß or r = γ – ß ……(ii)
According to the Snell’s law, \(\frac{n_2}{n_1}\) = \(\frac{\sin i}{\sin r}\)
When angles i and r are very small, then sin i = i and sin r = r
\(\frac{n_2}{n_1}\) = \(\frac{i}{r}\)
Substituting the values of / and r from Eqs. (I) and (ii), we get
n1(α + γ) = n2(γ – ß) …..(iii)
If the aperture of the spherical surface is small, then angles α, ß and γ will be small and point N will lie near to pole P.

(b) Sign convention: The distance measured from pole in the direction of propagation of light rays are taken positive and distances measured from pole in opposite direction of propagation of light rays are taken negative.
Heights measured above the principal axis are taken positive and that below the principal axis are taken as negative.

(ii) No, it is because in lens Maker’s formula,
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) = (μ – 1)[\(\frac{1}{R_1}\) – \(\frac{1}{R_2}\)]
= -(μ – 1)[\(\frac{1}{R_2}\) – \(\frac{1}{R_1}\)]
i.e. On reversing the lens, values and signs of R₁ and R₂ get reversed. Thus, for a given position of object (u), position of image (v) remains unchanged.

Question 33.
(i) An AC voltage V = V_m sin ωt is applied across an inductor of inductance L. Find the instantaneous power P_i supplied to the inductor. Show graphically the variation of P_i with ωt. [2]
(ii) Three electrical circuits having AC sources of variable frequency are shown in the figures. Initially, the current flowing in each of these is same. If the frequency of the applied AC source is increased, how will the current flowing in these circuits be affected? [3]
Give the reason for your answer.

(i) Resonance frequency of a circuit is v. If the capacitance is made 4 times the initial value, find the change in the resonance frequency. [1]
(ii) A 100 Ω resistor is connected to 220 V, 50 Hz supply.
(a) What is rms value of current in the circuit? [1]
(b) What is the net power consumed over a full cycle? [1]
(iii) A 2 μ F capacitor, 100 Ω resistor and 8 H inductor are connected in series with an AC source. [2]
(a) What should be the frequency of the source such that current drawn in the circuit is maximum? What is this frequency called?
(b) If the peak value of emf of the source is 200 V, find the maximum current.
Answer:
(i) In an inductor, the current lags the voltage by 90°. If the source voltage is sinusoidal, then the current is also sinusoidal, but shifted in phase. The instantaneous power defined as the product of the instantaneous voltage and current can also be seen to be sinusoidal in time. However, in contrast to the resistive load, the instantaneous power in the inductor goes negative for part of the cycle of the source driving it.
As, V(t) = V_m sin ωt
I(t) = -I_m cos ωt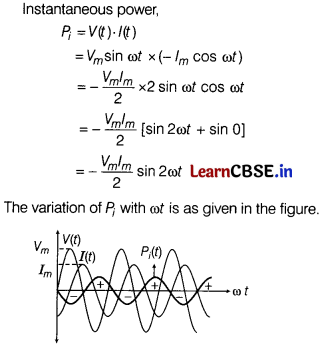

The instantaneous power alternates positive and negative at twice the frequency of source supplying it.

(ii) Let initially, I_r be current flowing in all the three circuits. If frequency of applied AC source is increased, then the change in current will occur in following manner.
(a) AC circuit containing resistance only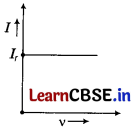

There is no effect on current with the increase in frequency.

(b) AC circuit containing inductance only: With the increase of frequency of AC source, inductive reactance increases as
X_L = ωL= 2πvL
I = \(\frac{V_{\mathrm{rms}}}{X_L}\) = \(\frac{V_{\mathrm{rms}}}{2 \pi v L}\)
For given circuit, I ∝ \(\frac{1}{v}\)
Current decreases with the increase in frequency.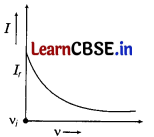

(C) AC circuit containing capacitor only
X_C = \(\frac{1}{\omega C}\)= \(\frac{1}{2πvC}\)
I = \(\frac{V_{\mathrm{rms}}}{X_C}\) = \(\frac{V_{\mathrm{rms}}}{\left(\frac{1}{2 \pi v C}\right)}\),
I = 2πvCV_rms
For given circuit, I ∝ v
Current increases with the increase in frequency.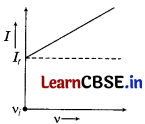

Or

(i) As, resonance frequency,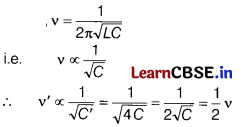

(ii)
(a) Given, R = 100 Ω, E_rms = 220V, v = 50 Hz.
rms value of current, I_rms = \(\frac{E_rms}{R}\)
⇒ I_rms = \(\frac{220}{100}\) =22 A

(b) Net power consumed,
P_av = E_rms I_rms = 220 × 2.2 = 484 W

(iii) (a) Given, capacitance,C =2 μF = 2 × 10^-6F
Resistance, R = 100 Ω
Inductance, L = 8 H
Peak value of voltage, E₀ = 200 V
When frequency of AC source is equal to resonant frequency, then current drawn in the circuit is maximum.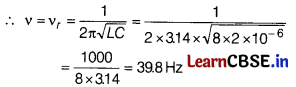

(b) ∴ I₀ = \(\frac{E_0}{R}\) = \(\frac{200}{100}\) = 2 A